
This article is in continuation of this one.
Recap
In the previous article, I had tried to emphasize how
nᵗʰ Fibonacci Number = Number of ways to climb n step staircase, where you have only two possible options to move, either by climbing 1 step or 2 steps at a time.
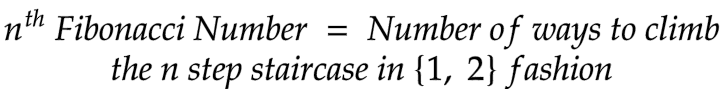
In the same article, I have mentioned some other possible representations of the Fibonacci Sequence. One of them is the number of ways to tile a N x 1 board with a 1 x 1 square and 2 x 1 domino. By writing the recurrence relation for the same, we can state that NoOfWaysToTile(n) = nᵗʰ Fibonacci Number.
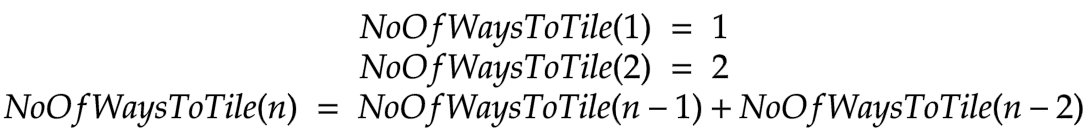
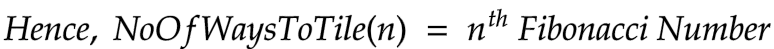
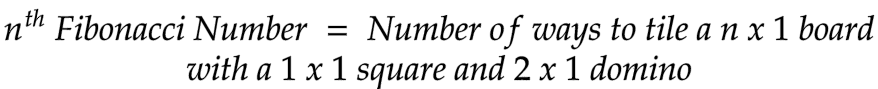
In this article, I am going to discuss my approach to the Running Sum Identity of the Fibonacci Sequence using the same relation.
The Running Sum of Fibonacci Sequence
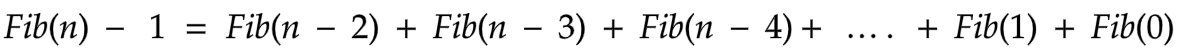
The Left Hand Side (L.H.S.)
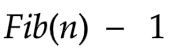
The L.H.S. of the equation has 2 parts Fib(n) and (- 1).
Fib(n) = nᵗʰ Fibonacci Number = No of ways to tile n x 1 board.
But what does this ‘one’ represent?
Since everything in this relation is related to ‘the number of ways to achieve tiling’ then this ‘one’ can only represent a scenario. That scenario can be ‘the occurring some specific event’, say E, and this event E can only occur once. The negation sign before ‘one’ is actually excluding the possibility of happening of this event E.
Now L.H.S. = No of ways to tile n x 1 board - Occurring of the Event E.
In other words, L.H.S. states the number of ways to tile the board without the occurrence of that special event E.
What can E be?
The only thing special about E was that it can happen only once, in any scenario, it means that whatsoever be the size of the board, the E can only and only occur once.
Generally, these kinds of cases are very basic or formally known in Mathematics as trivial.
On the basis of all the facts and assumptions
- E has to have occurred only once.
- E hints to be a trivial case.
Finally, after looking at all the types of patterns, I assumed that E should be a case where we tile the whole board using only squares. I wasn’t sure but yes it worked.

E = the event when we tile the whole board with squares only.
“Clearly this can occur only once whatsoever be the value of n.
And kind of the case was trivial also.” — in support of my assumption.
Back to L.H.S.
Now L.H.S. becomes the total number of ways to tile the board excluding the case where we tile the whole board with 1 x 1 square, without using any domino.
Or, L.H.S. is the number of ways to tile board with at least one domino being used somewhere.
This second interpretation actually helped in deducing the other side of the equation
The Right Hand Side of the Equation (R.H.S.)
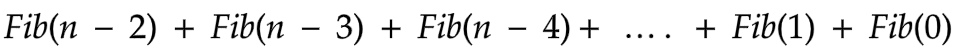
Now, it was clear that if I am able to emphasize that this summation says the same story as the latter meaning of L.H.S., then the job is done.
L.H.S. says that
“ I am the number of ways to tile board with at least one domino being used somewhere.”
Let us take some close observation on the summation
- Each term in the summation is a positive term, hence no exclusion is happening in this part of the equation
- Since there is no term with a minus sign, then each of the terms in the expression is a representation of a case, and all the cases are mutually exclusive (i.e. no two cases overlap)
- And the summation of all the terms gives the total number of ways to perform the act, this means that the cases are exhaustive(i.e. covers all possibilities)
The First term: Fib(n - 2)
Fib(n - 2) represents the number of ways to tile (n - 2) longboard.
Since we have 2 tiles of the board empty and Fib(n - 2) solely doesn’t guarantee that a domino will come at least while tiling the whole n x 1 board, we can put the domino at the very beginning.
The First Term = Number of ways to cover the whole board with the first domino placed at the first-second tile = 1 * Fib(n - 2) = Fib(n - 2)

The Second Term: Fib(n-3)
Taking inspiration from the first term we can say that in the second term should count the cases when the first domino is placed at the second-third tile. So the first tile should obviously be tiled with a square.
The Second Term = Number of ways to cover the whole board with the first domino placed at the second-third tile
or The Second Term = (Number of ways to tile the 1 x 1 board with only squares) * (Number of ways to place domino at second-third tile) * (Number of ways to tile rest of the board, the board of length n - 3)

The Third Term: Fib(n-4)
Following the induction
The Third Term = Number of ways to cover the whole board with the first domino placed at the third-fourth tile
or The Third Term = (Number of ways to tile the 2 x 1 board with only squares) * (Number of ways to place domino at third-fourth tile) * (Number of ways to tile rest of the board, the board of length n - 4)

The Kᵗʰ Term: Fib(n - (k + 1))
The Kᵗʰ Term = Number of ways to cover the whole board with the first domino placed at the kᵗʰ — (k+1)ᵗʰ tile
or The Third Term = (Number of ways to tile the (k - 1) x 1 board with only squares) * (Number of ways to place domino at kᵗʰ - (k+1)ᵗʰ tile) * (Number of ways to tile rest of the board, the board of length n - k - 1)

Hence each of the terms in the summation represents a case when the first domino is placed at a specific position. These cases adhere to the rules of being mutually exclusive and forming an exhaustive set.
Hence we can say that R.H.S. also represents all the ways to tile the board at least using a domino.
Finally, it’s done.
Hence we can say the Running Sum of the Fibonacci Sequence equates the number of ways to tile the n x 1 board with using at least one domino, using two different methods of counting, known as the inclusion-exclusion principle and exhaustive counting.
Next time you encounter a problem that requires you to add the terms of the Fibonacci Sequence just remember the story, you will not need to remember the formula. And I think that if we change the dimensions of the tiles being used here, still we can derive a relation of this kind, with newer tiles or for a sequence somewhat similar to the Fibonacci Sequence.
Towards the End…
The article is verbose and overexplained at a lot of places. But I had to put down what all things came to my mind while looking at the equation and finding out what it actually emphasizes. I thought if I’ll put up the solution directly then most of the things will seem magical and most of you will believe that I just crawled on the net for two days and copy-pasted it here.
Yes, I haven’t used the climbing stairs interpretation because I wasn’t comfortable with it in the beginning. Later, I thought it would be easier to put things the way they occurred to me rather than translating to some other problem, that too with no help in explanation.
I had seen my teachers explaining to us some complex mathematical formulas of combinatorics (nCr, nPr) using interpretations like these. They used to build a thought around the basic series first, this would generate a world (imagination) with rules. Then, they would try to explain what a formula, proven identity, or statement of a related theorem of the sequence will actually represent in that world and is actually valid using simple mathematical tools like set theory and basic counting. Here I have tried the same.
Dedicated to Dr. Saurabh Priyadarshi, Mr. Anshul Singhal and Mr. Anshul Tomar
And after a very long ending note,
Ram Navmi ki Shubhkamnayen
Bye :)








Comments
Post a Comment