Skip to main content

Climbing the Fibonacci Sequence

 

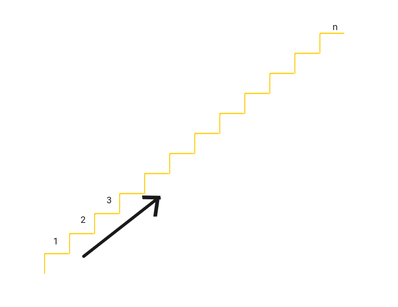
Image for post
Climbing Staircase Problem

The Story begins with a Problem
Yesterday, I was solving a very famous DP problem, the climbing stairs.
The problem is quite simple. You are climbing a staircase. It takes n steps to reach to the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Solution
The solution is also pretty straight forward.
Suppose we have climbed up some steps and we are left with some i steps to reach the top. Let’s say, NoOfWays(i) be a function that returns the number of ways to climb i steps to reach the top.

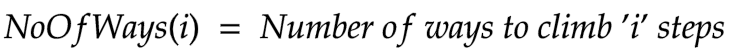
Image for post

If we climb by 1 step, then we are left with (i-1) steps. Using the above formula, the number of ways to climb (i -1) steps = NoOfWays(i-1).
Similarly, if we climb by 2 steps, then we are left with (i-2) steps, and using the formula, the number of ways to climb (i -2) steps = NoOfWays(i-2).
Since we can climb in one of the two fashions only so the number of ways to climb i steps is given as follows

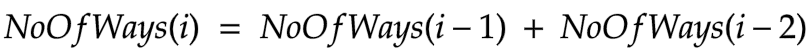
Image for post

For the base cases, we know
NoOfWays(1) = 1 and NoOfWays(2) = 2, therefore we can say

Image for post

With this recurrence relation, we can determine the number of ways to climb n steps to reach the top. Formally this solves the problem.

Now the solution and everything is fine but what is so special about this problem?
The answer is the result.

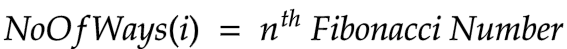
Image for post

On reversing the above equation, we can state that

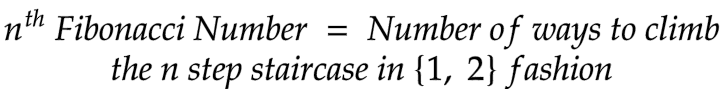
Image for post

Using the above representation of the Fibonacci numbers we can prove various identities and rules associated with the Fibonacci sequence.

Let’s say, Fib(n) represents the nᵗʰ Fibonacci Number.

The Convolution Theorem

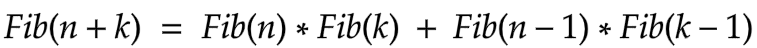
Image for post

Clearly the left-hand side of the equation represents the number of ways to climb the (n + k) stairs.
The task of climbing (n + k) stairs can also be completed in one of the two ways.

  • Case #1: If we step onto the nth step every time we climb
  • Case #2: If we skip the nth step every time

In Case #1,

Image for post

Since we stepped onto the nᵗʰ step. Then we must have climbed n steps in NoOfWays(n) ways, and are left with k steps to climb further.
Number of ways to climb = NoOfWays(n) * NoOfWays(k)

In Case #2,

Image for post

Since we skipped the nᵗʰ step. Then we must have climbed to the (n-1)ᵗʰ step and jumped to the (n + 1)ᵗʰ step.
Hence, Number of ways to climb = NoOfWays(n-1) * NoOfWays(k-1)

The cases discussed above are mutually exclusive (i.e. there can’t be a path which exists in both of the cases simultaneously) and exhaustive to the space of possibility (i.e. the total number of ways to climb the whole staircase)

We can say that,

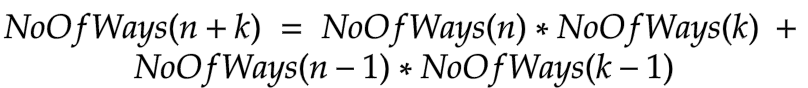
Image for post

Since NoOfWays(n) = Fib(n), therefore

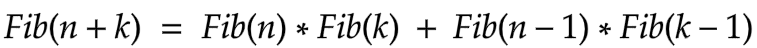
Image for post

This proves the Convolution Theorem of Fibonacci Number.

Further insight
Putting k = n and k = n +1 in the above equation,

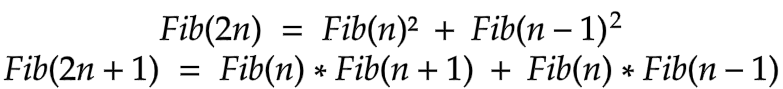
Image for post
Image for post

T(n) = 2*T(n/2) + O(1) when n is even
T(n) = 3*T(n/2) + O(1) when n is odd
Using the above results we can compute nth Fibonacci Number in O(log²N).

Similarly, we can derive the following summations on the Fibonacci Sequence using this representation method (I assume this, I haven’t thought of it yet)

  • Running Sum, Fib(n) + Fib(n-1) + Fib(n-2) … + Fib(0) = Fib(n+2) -1
    (UPDATE: link to my intrepetation of this formula is available here)
  • Sum of Even terms, Fib(0) + Fib(2) + Fib(4) …. + Fib(2n) = Fib(2n+1)

Some other representations that I found useful

  • Fib(n) = Number of ways to get a sum (= n) using only 1s and 2s.
  • Fib(n) = Number of ways to tile an n x 1 board using a 1 x 1 square and 2 x 1 domino (another DP problem)
Image for post

Towards the End…
All of this hit me while trying a question, that was easy and I already knew the logic and solution to but, till then I haven’t seen it the other way round. Then, I looked up for some popular properties on Google and tried it on them, and it worked out.
The idea isn’t unique and there might be some better representation of the sequence, that must have already been discussed before. But I found it cool, so I shared it with you. I also believe that representation like this helps in solving similar problems with complex modifications, that are difficult to decode using only mathematical equations. I hope you like the idea.

That’s my part
Signing off

Comments

Post a Comment

Popular posts from this blog

CodeChef March Challenge 2021 — Consecutive Addition

“You are given two matrices A and B, each with R rows (numbered 1 through R) and C columns (numbered 1 through C). Let’s denote an element of A or B in row i and column j by A(i,j) or B(i,j) respectively….. ” You can read the whole problem here . Problem description in short Given two matrices, A and B. Task is to transform A to B using special some addition-based criteria. The criteria for transformation is as follows we are given a number K 2 ≤ K ≤ min(R, C), where R is row size and C is column size we have to take any submatrix of size Kx1 (i.e. along the column) or 1xK (i.e. along the row), in A, and to all the numbers that fall under that submatrix have, add some integer v, this can be chosen by us. This has to be done in such a way that finally A transforms to B. The actual problem is to check if this kind of transformation is possible, given A and B. Ideation…. Befor e  I begin I wanna say that it is an observation based problem, can have many solutions and my solution is no...
2 comments
Read more

Fibonacci Sequence: Running Sum

  This article is in continuation of  this one . R ecap In the  previous article , I had tried to emphasize how nᵗʰ Fibonacci Number = Number of ways to climb n step staircase, where you have only two possible options to move, either by climbing 1 step or 2 steps at a time. In the same article, I have mentioned some other  p ossible representations of the Fibonacci Sequence. One of them is the number of ways to tile a N x 1 board with a 1 x 1 square and 2 x 1 domino. By writing the recurrence relation for the same, we can state that NoOfWaysToTile(n) = nᵗʰ Fibonacci Number. Recurrence for the Tiling problem Tiling Problem Relation and Fibonacci Number Reversing the above Equation In this article, I am going to discuss my approach to the Running Sum Identity of the Fibonacci Sequence using the same relation. The Running Sum of Fibonacci Sequence The Left Hand Side (L.H.S.) The L.H.S. of the equation has 2 parts  Fib(n)  and  (- 1) . Fib(n) = nᵗʰ Fibonac...
Post a Comment
Read more

Chocolate in the Boxes

Counting problems have been irritating people for ages. They are generally long and weird with additions — substractions going on in different parts with meanings difficult to understand. Out of all the popular counting problems, one can be solved using some chocolates and boxes, which I am going to discuss in this article. The Problem For the given equation, find the number of ways such that a, b, c, d has a whole number solution, i.e. a, b, c, d ≥ 0. Most of you might know the formula for the pr o blem, here we are going to discuss a thought on how to tackle such a problem and formulate it as people find it tough to memorize and often forget. Before discussing further let’s see what the chocolate problem is. The Chocolate Problem Let’s say, we have 10 chocolates, that we need to put in 4 different boxes. It is assumed that all the chocolates are identical, and we are asked to count the number of ways to put the chocolates into the boxes. Putting no chocolates at all into the box is t...
Post a Comment
Read more