Solving a Tree Problem

Balanced Binary Tree

Tree problems are quite popular among competitive programming questions. All the fame is because of the complexity of thought they deliver to the mind of a beginner and sometimes they even scare the intermediate programmers, who have been programming for a while.

Here in this blog, I will discuss a general problem that has similar complexity issues and share a thought to break the solution.

Some Prerequisites
Sites all over the internet are filled with basic level tree problems like

• Finding the depth of a node in a tree
• Finding the height of a tree
• Sum of a subtree rooted at some internal node of the tree
• Finding LCA (Lowest Common Ancestor)of two nodes of a tree (in O(N))
• Finding LCA of any two nodes of a tree (in O(logN))

Generally speaking, all such problems are the building block for the tree-problems of intermediate level, like one discussed below.

A Generic Problem
The problem starts with a description of a tree and clearing out what all kind of trees exist in this world, and then they quote a problem, which obviously can’t be solved with easy tree traversal approaches under given constraints, as

Assume that u and v are two nodes of a balanced binary tree with some given value ‘u’ and ‘v’ and dist(u, v) represent the distance (path length) between the nodes u and v in the tree. For all possible pairs of u and v formulate the expression given below

Constraints
Let N be the number of nodes, then N ≤10⁵.
With this, a modulus operation with some large prime is also applied onto the function to avoid overflows in the predefined datatypes in languages like C++ and Java.
This is the section where the real problem begins, and the hope of a beginner dies. O(N² * N) is the best approach that comes to the mind and then sticks there until you decide to leave the question.

Solving the problem
Before actually approaching the solution, I would like to enlighten you how experience helps in solving such problems and make them easy to break:

• A pool of previously solved problems exists inside your brain, from where you can fetch a few hints to approach a problem
• You already know names of some already existing algorithms, that you must have searched while solving problems with weird complexities and use them for your benefits
• You build an attitude that even if I am not able to solve it this time but next time I will have this problem in my pocket for tearing down some other problem of similar structure
• It helped me learn that a tree problem directly involving all the nodes can’t be solved in less than O(N) and always keep a tree in mind while solving the problem. Actually taking the input for the tree takes O(N) complexity wise. So don’t hope for miracles, unless there’s a catch in the statement. Yes, I was dumb.

So as I said solving intermediate-level tree problems takes experience so here are some anchors from my pools of experience that helped me solve the problem

• In tree problems involving the distance of a node from anywhere is somewhere related to its parent or ancestor, and especially, in the case of pairs of nodes, the LCA (Least Common Ancestor) is that special ancestor that can help in solving the problem
• I knew that Google can answer my questions like ‘How to find LCA in less than O(N)?’, and this time I also knew the algorithm beforehand. Hint: search Binary Lifting.
• Secondly, the question tempts me to directly do a direct DFS/BFS from node u to node v to find the distance, hence it's obvious that I should not do, it’s a trap. For all pairs as DFS/BFS has the time complexity of O(N) and in total O(N²) pairs exist in the tree.

With all these thoughts in mind, I started to modify the formula, as follows

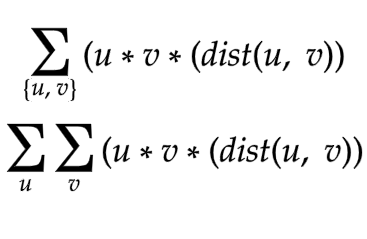
• Taking all the possible node u with all possible node v, broke the big summation into two. Finally, we would have an answer for {u, v} and {v, u} both adding up in the resultant, so just halving the resultant would have given the final answer.
• Now in a tree, there exists a single path from a node to another, that obviously passes through their LCA. Assuming that the LCA of a valid pair of nodes u and v is L, I split the dist(u, v) = dist(u, L) + dist(L, v) where LCA(u, v) = L.

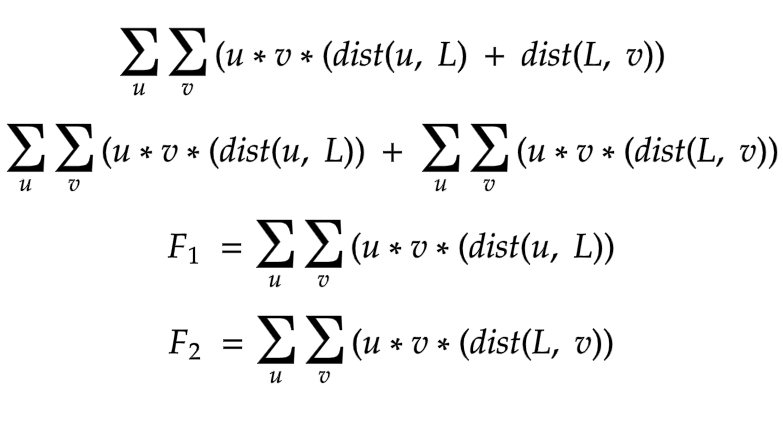
• Then, I had 2 similar looking parts of the formula, F1 and F2. Obviously, F1 = F2.
• On observing the formula F1 and the tree carefully, it becomes clear that for a given node u and L, some part of the formula is independent of the direct relation between u and v. Actually a relation between a subtree and u is established rather than a single node v, via L.

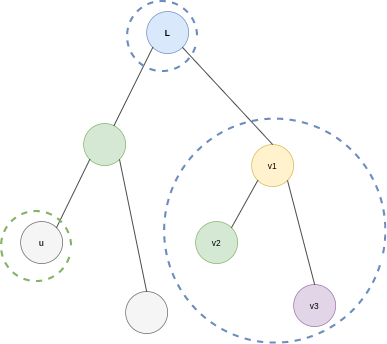
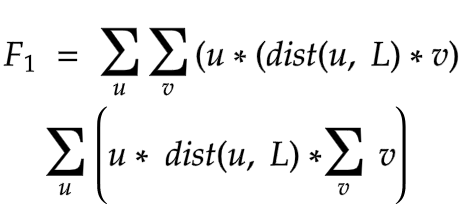
• Here the relationship between u, L and v can be exploited. The inner summation of v is actually summing of all the node values with ‘vi’ such that LCA of u and vi’s is L.
  In other words LCA(vi,u) = L where i = 1, 2, 3….

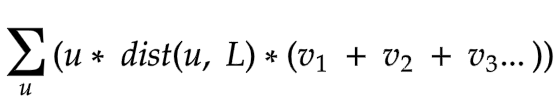
• Hence the summation on v is the sum of values in the subtree of L, not containing the node u.
  This summation can be precomputed for each node of the tree using some general traversal technique in O(N). Actually, this was the first time it hinted to me that I am proceeding in some right direction and solving simple questions like that paid.
• Now I could say that the new formula depended upon u and L rather than u and v

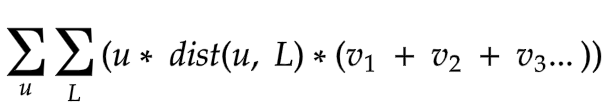
• How did this dependency actually help in solving the problem?
  For answering this we need to understand, what all nodes can be ‘L’ for a given node u.
  Here, L can be any potential node that is parent or ancestor of u. So the complexity for solving for each node is now dependent upon the number of parents of a node. And here’s a catch, the tree given is a balanced binary tree so maximum ancestors a node can have is log(N). This simple catch was the final hint and the whole of the question just broke inside my head.

Since the total number of nodes present in the tree is N and at the max, a node can have log(N) parents so the time complexity for solving the expression for the tree is O(N*logN), prefect for N ≤ 10⁵.

After this just properly formulate the summation with all the needed requisites like subtree sum etc. And it’s done!

From my side…
Refraining myself from the ideal editorial-sequence, that first discusses a solution for smaller N (ie N ≤ 10³) and then jumping onto the main constraints, I chose to directly discuss the problem’s solution because I think that sometimes it’s just not worth it. Solving for some relaxed constraints doesn’t always give you some hints for further advancements until it’s a DP or subset problem, it’s just an approach, not a solution. And I feel while understanding something new, learning the flow of thoughts is also important, the flow of how people think, observe and apply. If I waste time reading solutions for relaxed constraints I won’t be able to learn how people hit the bigger problem in one go without solving for subparts separately, and this is important for confidence.

That’s my part
Signing off