
Counting problems have been irritating people for ages. They are generally long and weird with additions — substractions going on in different parts with meanings difficult to understand.
Out of all the popular counting problems, one can be solved using some chocolates and boxes, which I am going to discuss in this article.
The Problem
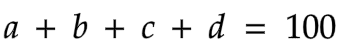
For the given equation, find the number of ways such that a, b, c, d has a whole number solution, i.e. a, b, c, d ≥ 0.
Most of you might know the formula for the problem, here we are going to discuss a thought on how to tackle such a problem and formulate it as people find it tough to memorize and often forget. Before discussing further let’s see what the chocolate problem is.
The Chocolate Problem
Let’s say, we have 10 chocolates, that we need to put in 4 different boxes. It is assumed that all the chocolates are identical, and we are asked to count the number of ways to put the chocolates into the boxes. Putting no chocolates at all into the box is totally acceptable.
Approach
To solve this problem we will put all the chocolates onto a table in a line and use three identical separators or ‘verticles’ with them.

The verticles separate the chocolates into different sections. Chocolates that lie between two verticles can go into a box.
For our problem let us assume that the chocolates to the left of the first verticle can go into the first box, those which are lying between the first and second verticle will go into the second box and similarly, chocolates lying between second and last verticle will go into box number three and the rightmost bunch of chocolates goes into the fourth box.
From here we can say that the number of ways to arrange these 10 chocolate and 3 verticles can give us the solution to the problem.
But wait, will all arrangements be valid.
Yes, with a simple demonstration we can show that all the arrangements generated are valid for solving the problem. Some of the weird arrangements are shown below. Remember that the boxes can be left empty.

In Arrangement 1, the first and second verticle come side by side. Hence it represents the case when no chocolate goes into the second box. Hence the second box remains empty.

In Arrangement 2, the first and fourth box remains empty, as there are no chocolates left on another side of the first and last verticle.

Similarly, in Arrangement 3, all the 10 chocolates go into the first box, and all the other three boxes go empty.
Now the question is reduced to count the number of ways to arrange the things lying on the table.
The formula to count the number of ways to arrange N things is ‘N!’
And the formula to count the number of ways to arrange N, things out of which R are identical is (N!/R!).
Now for our problem, we have assumed in the beginning that the chocolates and verticles are identical to their respective kind. Hence the number of ways to arrange these 10 identical chocolates + 3 identical verticles is
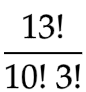
The above formula can also be represented as
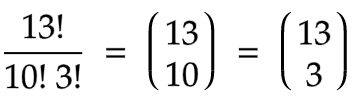
Hence the result is the answer to the given chocolate problem.
Suppose in a more general case we had n chocolates and k boxes then, to solve the problem we would have used k -1 separators. Then we would have n+k-1 total objects on the table. Hence the solution to this general case would have been
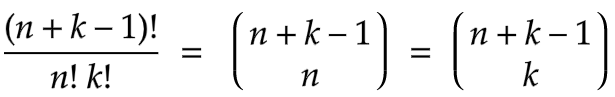
Observation
If we compare our original problem to the chocolate problem, we can use each of our variable (i.e. a, b, c, d) as one box and let the total number of chocolates be 100, then using the same technique we can solve the problem of finding all possible ways to assign a whole numbers to each variable. That’s it.
So rather than memorising a scary formula without meaning, it’s better to learn a technique to formulate it. This helps in two ways:
- You cannot deduce the formula wrong if you imagine things in the right way. In case you have memorized it, then you can always verify it.
- You can handle a lot of variation to the same problem easily, just by closing your eyes and taking examples.
And next time you meet a complex or irritating combinatorics formula, then you can say that there must be an interesting story behind it too, or you can write one of yours!
Signing off





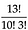


Comments
Post a Comment